Data structures and complexity
In this session we will introduce some of the useful data structures available to you in rust. I don't have a good definition of a data structure, but would roughly define them as any struct or type which organises a collection of data and gives efficient access to it.
We'll also more talk more about computational complexity, picking back up from its use in sessions one and two.
We will start with some more abstract definitions with short exercises and questions, then go through a worked example. This time, a k-mer counter.
- Introduction to rust data structures
- A practical example: counting k-mers from sequencing reads
- Further thoughts and reading
Introduction to rust data structures
Lists (Vec)
The foundational data structure is the list, i.e. Vec. We've already used this,
but to recap:
let mut x = Vec::new()makes an empty list calledx.x.push(32)adds the value 32 to the back of the list.x[0]accesses the first element of the list.x[0..3]would access elements 0,1,2.x.pop()removes and returns the last value of the list (first in last out i.e. a stack).
To understand data structures a bit better it's worth thinking about how this works under the hood. The list is stored in memory which is managed by the operating system (specifically, the heap, which can grow and shrink). The memory has to be requested from the operating system with an allocation call (memory allocation -- malloc) which requires a specific size to be specified. When you are done with it you need to return the memory to the operating system with a call to 'free'. In rust (or C++) it is rare to do this manually as they are handled by the data structure implementations (whereas in C you have to do make these calls yourself).
When you make a new Vec there will be a guess about its size which sets the
initial allocation request. This may be longer than the amount actually used by the list which allows more
elements to be added later. The allocated size can be checked with .capacity() and
increased manually with .reserve(). The size of the Vec can be checked with .len()
and may be lower than the capacity:
#![allow(unused)] fn main() { let mut x = Vec::with_capacity(5); x.push(1); x.push(1); println!("list: {:?} size: {} capacity: {}", x, x.len(), x.capacity()); // x = [1, 1] // the memory allocated for x is [1, 1, NA, NA, NA] }
When you access an element with e.g. x[3] what happens underneath is that x
contains a pointer to the start of the list which is a memory address. Then three times
the length of each list item is added to this (i.e. three times one byte if the list was u8,
three times eight bytes if the Vec was of f64), and that value at that memory address
is loaded into the CPU registers. As the value is directly accessed and the method
to find the address is independent of the length of the list, this operations is O(1)
which is constant time.
Question: what is the average time it would take to find a value in this list?
What happens when you push a value to a list which is already at capacity? The capacity
must first be increased. If there is space
next to the existing list in memory then empty allocated space can be added on at
the end, but otherwise an entirely new area needs to be allocated, the old list copied
across to the new space, and the old space freed. Clearly this can be inefficient
so should be avoided. One reasonable strategy you don't know the upper bound
is to double the capacity each time (i.e. exponential increase). Ultimately the
Vec and its methods will manage all of this for you and will usually be very efficient.
When you know the capacity exactly, you can set it when first allocated, but setting
the wrong capacity can lead to degraded performance.
Try running the code below to see how the size and capacity change as the list grows:
#![allow(unused)] fn main() { let mut x = Vec::with_capacity(2); x.push(1); x.push(1); println!("size: {}\tcapacity: {}\tlist: {:?}", x.len(), x.capacity(), x); x.push(1); println!("size: {}\tcapacity: {}\tlist: {:?}", x.len(), x.capacity(), x); x.push(1); println!("size: {}\tcapacity: {}\tlist: {:?}", x.len(), x.capacity(), x); x.push(1); println!("size: {}\tcapacity: {}\tlist: {:?}", x.len(), x.capacity(), x); }
Binary trees
We asked how long it would take to find a value in the list. For a list with N elements it will take N/2 accesses and comparisons on average, or N if the search is not in the list.
This is a common task which we could probably come up with a better strategy for. What about if we sorted the list first? (NB: sorting has \(N \log N\) complexity). Then for each search we would be able to use whether the comparison was higher or lower to tell us about where to search next. If we split the sorted data 50:50, then each of these new splits 50:50 and so on recursively we create a binary tree. Now, we compare our value to the root of the tree, and if it is lower search the left subtree, if higher search the right subtree. If it matches or we reach a terminal node the search is over.
Question: what is the complexity of finding a value in a binary tree?
In rust, the implementation to use is BTreeMap which deals with some of the practicalities
of caching in a slightly more complex data structure to achieve this, but still using
the same overall idea. Its interface is very simple to use:
#![allow(unused)] fn main() { use std::collections::BTreeMap; let mut bus_capacity = BTreeMap::from([ ("NC", 38), ("SC1", 25), ("SC2", 20), ("SW", 15), ]); bus_capacity.insert("CC1", 45); let to_find = ["SW", "NC1"]; for bus in &to_find { match bus_capacity.get(bus) { Some(capacity) => println!("{bus} route has capacity {capacity}."), None => println!("No such route as {bus}.") } } }
See the docs page for more examples.
Hash tables (dictionaries)
The binary search has complexity \( \log_2 N\). Can we do any better? Yes! A hash table, which you might better know as a dictionary, has constant complexity O(1) for looking up values. How does it achieve this?
Each key is passed through a hash function. Hash functions produces integers which are uniformly distributed. A simple hash function which would produce integers in the range 0-100 would be \( \mathrm{mod}_{100}((x + 10) * 7)\). As anything in a computer is ultimately a number, it's usually possible to hash complex structs by decomposing them down to their fundamental types and combining them.
These hash values then give the index for entry into a Vec. So if we made a Vec
with capacity 100 and used the above hash function, then added keys 'H',
'He' and 'Ne' using the above hash function on each character we'd get:
H -> (72 + 10) * 7 mod 10 = 74
He -> 81
Ne -> 23
We store both the key and the associated value in the table, so if we were storing atomic weights we'd enter these at index 74 for Hydrogen, 81 for Helium and 23 for Neon. You can see that the list is not in order. But now if we want to search for Helium, we simply calculate its hash function (81) and look up that index. This doesn't depend on the size of the dictionary so takes constant time.
Why do we store the key? It is possible that two keys map to the same index with the hash function so we need to resolve these. We won't got further into the details of this here, but it can be relatively simple to solve for example with 'linear probing'. One thing to know is that the closer the table gets to capacity the more likely these collisions are to occur, which makes lookup and addition to the table slower. Then the capacity needs to be reallocated and copied.
Using a dictionary in rust is almost identical to a BTreeMap:
#![allow(unused)] fn main() { use std::collections::HashMap; let mut bus_capacity = HashMap::from([ ("NC", 38), ("SC1", 25), ("SC2", 20), ("SW", 15), ]); bus_capacity.insert("CC1", 45); let to_find = ["SW", "NC1"]; for bus in &to_find { match bus_capacity.get(bus) { Some(capacity) => println!("{bus} route has capacity {capacity}."), None => println!("No such route as {bus}.") } } }
Exercise: Create a BTreeMap and HashMap with \( 10^7 \) entries of
pairs of random numbers (see the rand library
to generate these). How long does it take to access \( 10^5 \) of these entries
in each case?
You can time your code using:
#![allow(unused)] fn main() { use std::time::Instant; let start = Instant::now(); /// code goes here let end = Instant::now(); eprintln!("Done in {}ms", end.duration_since(start).as_millisecs()); }
You should find that the hash table is faster than the B-Tree. So why would you ever want to use the B-Tree? If the order of your values is important when you iterate through them, or you want to search for all keys within an interval, then the B-Tree is likely the better choice.
There are implementations of HashMap which can be faster, particularly if you are
not bothered about 'secure' hashing (which in most research applications, you are
usually not). One I like is hashbrown.
Maps and sets
If you don't need values associated with keys then you have a set. You can use
HashSet for this, which is equivalent to set() in python. For example, a set is a better
way than a list to keep track of values which you've already added to data.
Queues
Unlike Vec which is first in last out (FILO), queues are first in first out (FIFO).
So when you .pop() from a queue the front element is removed and everything comes
forward. These can be used as task schedulers in multiprocessing:
#![allow(unused)] fn main() { use std::collections::VecDeque; let mut queue = VecDeque::from(["long", "short", "basement"]); queue.push_back("short"); println!("{},{}", queue.pop_front().unwrap(), queue.pop_front().unwrap()); }
More complex to implement but useful for many algorithms is a priority queue, where each item is given a weight and the top weight will be served first:
#![allow(unused)] fn main() { use std::collections::BinaryHeap; let mut heap = BinaryHeap::new(); heap.push(1); heap.push(5); heap.push(2); println!("{}", heap.peek().unwrap()); // Find the top item but don't remove it println!("{}", heap.pop().unwrap()); println!("{}", heap.pop().unwrap()); }
Complexity of these data structures
There is a nice set of tables and guides in the documentation for std::collections.
Bitvectors
Sometimes you might want to keep track of a group of bits 0/1 rather than bytes (groups of eight bits). For example, if you were modelling a group of individuals you might include fields of information such as 'carer', 'child', 'infected' each of which are true or false.
You could use Vec<bool>? Actually, a bool is not a single bit and is a whole
byte set to zero or one. So if you have many bools this becomes inefficient.
Instead, you can use a bitvector from the bitvec
crate:
use bitvec::prelude::*;
let mut bv: BitVec = BitVec::new();
bv.push(true);
bv.push(false);
bv.push(false);
// bv is now an carer, adult, not infected
bv.set(2, true);
// bv is now infected
println!("carer: {} child: {} infected: {}", bv[0], bv[1], bv[2]);Strings
Strings are basically just a Vec<char> with a terminating character. However in rust String supports unicode
by default so we can do important things like:
#![allow(unused)] fn main() { let my_feelings = "😶"; println!("Current mood: {my_feelings}"); }
Otherwise the principles of capacity, resizing and element access are the same as for a Vec.
To demonstrate a more complex data structure, the 'famous' FM-index gives O(1) search of substrings within a string. This is useful for finding subsequences within genome sequences, which is normally very slow as it is linear time complexity in the length of the string. Modifying the example from the package docs:
use fm_index::converter::RangeConverter;
use fm_index::suffix_array::SuffixOrderSampler;
use fm_index::FMIndex;
// Prepare a text string to search for patterns.
let text = concat!("GGAGGTTACCTATGAAGAAGAAAAGAGTAGTGATTATATCCTTACTACTATTGTTAGTAA",
"GTGTCATTGGAATCAGTAGTTATTTTCTATTCAAGGATAAAATAAATCTGTTGGATGTAG",
"ACCATTCTGCCGTTGATTGGAACGGAAAAAAACAGAAGGATACAAGTGGAGAAGAAAATA",
"CAATTGCCATTCCAGGGTTTGAAAAAGTAACGTTGTATGCAAATGAAACAACACAAGCAG",
"TGAATTTCCATAATCCGGAAATTAATGATTGTTACTTCAAAATATCGCTTATTCATCCGG",
"ATGGTTCGGTTCTATGGATATCTGATTTAATCGAACCGGGAAAAGGTATGTATTCCATTG").as_bytes().to_vec();
let converter = RangeConverter::new(b' ', b'~');
let sampler = SuffixOrderSampler::new().level(2);
let index = FMIndex::new(text, converter, sampler);
// Search for a pattern string.
let pattern = "AAAA";
let search = index.search_backward(pattern);
// Count the number of occurrences.
let n = search.count();
println!("Found AAAA {n} times");
// List the position of all occurrences.
let positions = search.locate();
println!("Found AAAA at {positions:?}");The details of how the FM-index actually works is beyond the scope of this course.
Aside on string encoding
In high-performance genomics applications it is common to recode DNA bases {A, C, G, T/U}
to only take two bits rather than eight. A popular encoding is {0, 1, 3, 2} as you
can use the following functions to very quickly convert between char (equivalent to u8)
and back, and find the reverse complement base:
#![allow(unused)] fn main() { pub fn encode_base(base: u8) -> u8 { (base >> 1) & 0x3 } const LETTER_CODE: [u8; 4] = [b'A', b'C', b'T', b'G']; pub fn decode_base(bitbase: u8) -> u8 { LETTER_CODE[bitbase as usize] } pub fn rc_base(base: u8) -> u8 { base ^ 2 } // Creates a Vec<u8> which is C,G,T let bases = vec![b'C', b'G', b'T']; // Iterates over these bases, encodes them to two bits, and collects into a new vector let encoded: Vec<u8> = bases.iter().map(|b| encode_base(*b)).collect(); // Iterate backwards over the encoded bases, reverse complement the base, decode, and collect into a new vector let reverse_complement: Vec<u8> = encoded.iter().rev().map(|b| decode_base(rc_base(*b))).collect(); // String::from_utf8 makes a string from a Vec<u8>. We need to clone (copy) // it as otherwise it is moved and invalidated for future use println!("{bases:?} {}", String::from_utf8(bases.clone()).unwrap()); println!("{encoded:?}"); println!("{}", String::from_utf8(reverse_complement).unwrap()); }
These come from spotting some patterns in the ASCII codes for these letters:
| Letter | Code |
|---|---|
| A | 01000001 |
| C | 01000011 |
| G | 01000111 |
| T | 01010100 |
| a | 01100001 |
| c | 01100011 |
| g | 01100111 |
| t | 01110100 |
encode_base() bitshifts down by one position then masks all but the last two bases,
so essentially extracts bits two and three (highlighted above). rc_base() finds the
complement by an EOR (XOR) with 10, flipping the third bit above. This gives the mappings
00 (A) <=> 10 (T) and 11 (C) <=> 01 (G).
You sometimes
see Vec<u8> or &[u8] used for these applications. If you pack as many of these
two-bit DNA bases as possible into a 64-bit integer (the largest CPUs natively support)
you can store 32 bases. As we normally use odd numbered k-mers to avoid self-reverse-complement
sequences, this explains why k=31 is such a common choice.
A practical example: counting k-mers from sequencing reads
Background
In this example we will write some code to read in a fastq file and count k-mers from the sequencing reads within.
Download the following pair of fastq files from ENA: https://www.ebi.ac.uk/ena/browser/view/ERR8158023
A record in a fastq file looks like this:
@ERR556974.1 1_24_206_F3_03/1
CCATCTATCGATTGTTTGCCCATCAAAACCAAATCCGGTTTTTCATTAGCTACGATACTATTTAATATCTTGNNN
+
>>>;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;8..................((((((((((!!!
This is the forward sequencing read. The four lines are a read ID, the sequence,
a separator, and quality scores for each base (PHRED).
The reverse read will be found in the _2.fastq.gz file with the header @ERR556974.1 1_24_206_F3_03/2.
A very common task in genomics is to count the k-mers in the sequences. These are all the substrings of length k, for example the 5-mers in this read are CCATC, CATCT, ATCTA and so on. One thing we can use the k-mers for is to detect and remove or correct sequencing errors. We normally sequence to a certain coverage, for example 30x, which means on average 30 reads cover each position. So we would expect around 30 k-mers to cover each base. However if there is an incorrect base call in a read, we will find that the k-mers spanning that base are usually unique because the error has only happened in one read. So if we go through all of the k-mers in the input file and count the number of times we see them, we can find the error k-mers and the correct k-mers. The correct k-mers could then be used to assemble the genome, or you could remove every read which contains and error k-mer.
The full dataset is quite large for an unoptimised counter, so make a test set with only the first 10k reads from each file:
gzip -d -c ERR8158023_1.fastq.gz | head -40000 | gzip -c > test_1.fastq.gz
gzip -d -c ERR8158023_2.fastq.gz | head -40000 | gzip -c > test_2.fastq.gz
Counting with different data structures
In rust, the needletail crate gives a fast and easy to use method to read in fastq files:
extern crate needletail; use needletail::parse_fastx_file; fn main() { let mut reader = parse_fastx_file("test_1.fastq.gz").unwrap_or_else(|_| panic!("Invalid path/file")); while let Some(record) = reader.next() { let seqrec = &record.expect("Invalid FASTA/Q record"); println!("{:?}", seqrec.seq()); } }
So in the loop the seqrec.seq() gives access to the sequence in the read.
The return type is Cow<[u8]> which we haven't seen yet. 'Cow' means 'copy-on-write',
so it lets us use a reference if we just read the data, but if we modify anything
a copy will automatically be created so the original data isn't changed. [u8] is
an array of char i.e. the sequence. These are the 8-bit numbers, to get the actual
character from a variable x which is u8 you just need to use x as char.
You can also use seqrec.qual() to get the quality scores, but we will ignore these here.
So, to loop through the 31-mers in each read we could use:
#![allow(unused)] fn main() { let k = 31; while let Some(record) = reader.next() { let seqrec = record.expect("Invalid FASTA/Q record"); for idx in 0..(seqrec.num_bases() - k) { let kmer = seqrec.seq()[idx..=(idx + k)]; println!("{kmer}"); } } }
For the exercises, check they work on your test files. Then, time them on the full files (the first code will take around five minutes to run).
Exercise 1 As we don't know which strand was sequenced we also need to consider
the k-mer on the opposite strand. We need take the reverse complement and then
just use the 'lower' (by the < operator) of the two -- known as the 'canonical k-mer'.
Add a line which calculates the reverse complement of the k-mer and then outputs
the canonical k-mer at each position. It's easier if we convert to a String:
#![allow(unused)] fn main() { let mut kmer_counts: BTreeMap<String, usize> = BTreeMap::new(); let k = 31; // let filenames = vec!["ERR8158023_1.fastq.gz", "ERR8158023_2.fastq.gz"]; let filenames = vec!["test_1.fastq.gz", "test_2.fastq.gz"]; for filename in filenames { eprintln!("Parsing: {filename}"); let mut reader = parse_fastx_file(filename).unwrap_or_else(|_| panic!("Invalid path/file: {filename}")); while let Some(record) = reader.next() { let seqrec = record.expect("Invalid FASTA/Q record"); for idx in 0..=(seqrec.num_bases() - k) { let kmer = String::from_utf8(seqrec.seq()[idx..(idx + k)].to_vec()).unwrap(); let rev_kmer: String = kmer.chars().rev().map(|b| match b { 'A' => 'T', 'C' => 'G', 'G' => 'C', 'T' | 'U' => 'A', _ => 'N' }).collect(); let canonical_kmer = if kmer < rev_kmer {kmer} else {rev_kmer}; *kmer_counts.entry(canonical_kmer).or_insert(0) += 1; } } } }
Note the line *kmer_counts.entry(canonical_kmer).or_insert(0) += 1;. This uses
the .entry() API to the BTreeMap
which allows values to be modified or added depending on whether they are in the
map yet. In this case, if the entry is not yet found it is inserted with a value of 0. Then,
whether found or not, this count is incremented.
How long does this take to run on the full dataset? NB make sure to run your
code with the --release flag.
Exercise 2 At the end of this code, add a loop over the kmer_counts map
to count the number of k-mer sequences with each observed count. Print these
counts between 1 and 100. Then, plot a histogram
of these counts (using your favourite plotting package, probably matplotlib or R).
It should look something like this:
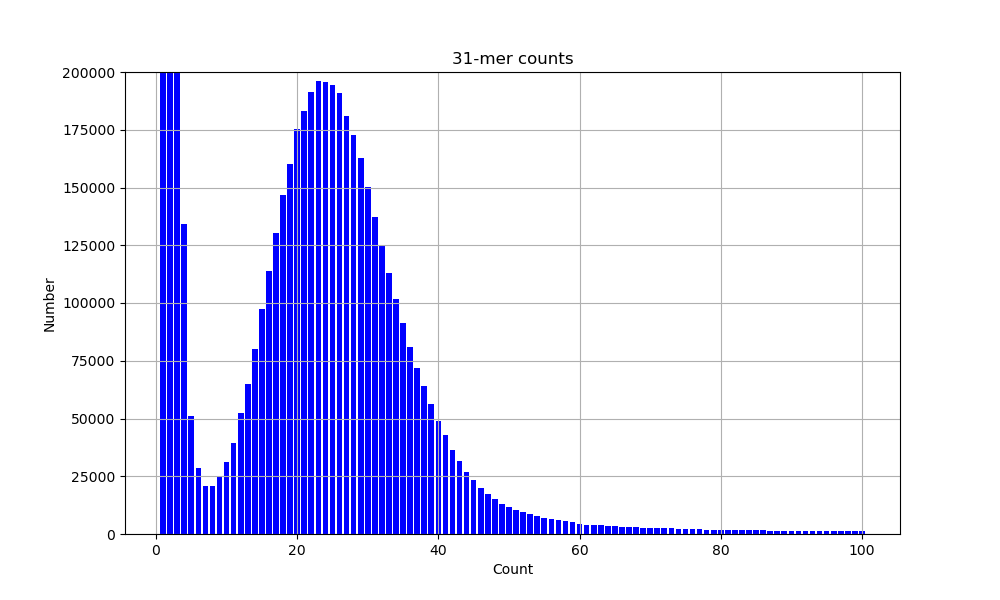
If you need help plotting, the python code for this can be expanded below.
Plotting code
import matplotlib.pyplot as plt
# Histogram data
data = [
(2, 15484361),
(4, 489010),
(6, 94724),
(8, 44768),
(10, 49707),
(12, 70508),
(14, 98919),
(16, 134835),
(18, 179460),
(20, 218909),
(22, 254678),
(24, 283570),
(26, 306604),
(28, 311785),
(30, 307007),
(32, 287181),
(34, 267382),
(36, 237045),
(38, 206375),
(40, 177546),
(42, 146763),
(44, 121426),
(46, 99932),
(48, 79153),
(50, 62170),
(52, 49436),
(54, 39272),
(56, 31315),
(58, 25672),
(60, 20977),
(62, 16362),
(64, 13319),
(66, 11578),
(68, 9804),
(70, 8140),
(72, 7398),
(74, 6501),
(76, 5969),
(78, 5420),
(80, 5036),
(82, 4370),
(84, 3992),
(86, 4143),
(88, 3854),
(90, 3898),
(92, 3799),
(94, 3424),
(96, 3135),
(98, 2923)
]
x_values, y_values = zip(*data)
plt.figure(figsize=(10, 6))
plt.bar(x_values, y_values, color='blue')
plt.title('31-mer counts')
plt.xlabel('K-mer count')
plt.ylabel('Count')
plt.ylim(0, 200000)
plt.grid(True)
plt.show()
Exercise 3 Time the main loop which counts the k-mers and separately time
the loop which prints them out. Then, change the BTreeMap to a HashMap. How do
the times change? Change the HashMap to the implementation from use hashbrown::HashMap;
instead of the std crate. How do the times change now?
Optimising the code
This is relatively computationally intensive. How can we do better? Firstly, if we use the code above to encode the k-mers as 64-bit integers, our dictionary will be able to access the elements much faster as hashing the computer's word size is a lot faster than a string of unknown length. Secondly, rather than taking a slice from the sequence each time we could instead try to 'roll' the k-mer through the read, as to get to the next k-mer we just need to remove the first base removed and add a new last base.
Change your code as follows:
pub fn encode_base(base: u8) -> u8 { (base >> 1) & 0x3 } pub fn rc_base(base: u8) -> u8 { base ^ 2 } fn main() { let mut kmer_counts: HashMap<u64, usize> = HashMap::new(); let k = 31; let mask = (1 << (k * 2)) - 1; let filenames = vec!["ERR8158023_1.fastq.gz", "ERR8158023_2.fastq.gz"]; for filename in filenames { eprintln!("Parsing: {filename}"); let mut reader = parse_fastx_file(filename).unwrap_or_else(|_| panic!("Invalid path/file: {filename}")); while let Some(record) = reader.next() { let seqrec = record.expect("Invalid FASTA/Q record"); let mut fwd_kmer: u64 = 0; let mut rev_kmer: u64 = 0; for (idx, base) in seqrec.seq().iter().enumerate() { let fwd_base = encode_base(*base); let rev_base = rc_base(fwd_base); fwd_kmer <<= 2; fwd_kmer |= fwd_base as u64; fwd_kmer &= mask; rev_kmer >>= 2; rev_kmer |= (rev_base as u64) << ((k - 1) * 2); rev_kmer &= mask; // Once the first valid k-mer has been filled if idx >= k { let key = if fwd_kmer < rev_kmer {fwd_kmer} else {rev_kmer}; *kmer_counts.entry(key).or_insert(0) += 1; } } } } // TODO: Counting and hist code go here }
This uses some of the bitshifting tricks we used in the first session.
Add your count code at the end. How long does the code take to run now?
Other data structures
Another data structure, beyond the scope of this introduction, is the
Bloom filter
which can determine whether an item is present in a set, but with a false positive
rate. If you would like to try this, there is an implementation in the bloom
crate.
Further thoughts and reading
Try profiling your code with flamegraph. What takes the longest? Reading the file, processing the sequence, or adding to the dictionary?
If you want to understand more about why the k-mer counting takes a long time you can read about the CPU cache in the algorithmica book, but be warned it is quite involved! A perhaps more lively demonstration of this issue is in this computerphile video.
A blocked-bloom filter is a more cache-efficient implementation. Using this as the first stage to filter singleton k-mers, followed by a dictionary for counting gives an error-free k-mer count that is around twice as slow as the best implementations. Parallelism can be used to improve this further.
For all of these dictionary-based implementations the complexity overall is
linear with the number of k-mers in the file. So while the total speed changes
by a constant factor, all take twice as long to run with twice as many reads
in the input (try reading just one of the fastq files to confirm this). What
about the BTreeMap?